Cálculo de los criterios de falla Hoek-Brown con python.

En este post, aplicaré el cálculo de los criterios de falla de Hoek-Brawn usando python.

Los afloramientos rocosos  no están formados solo por un gran bloque de roca intacta. Por lo general es un conjunto de bloques separados por fracturas y discontinuidades. Estas discontinuidades, cambian el comportamiento mecánico y la respuesta de la roca a las tensiones. 

Es por esto que en 1980 se introdujo el criterio de Hoek-Brown para proporcionar información fiable en el diseño de excavaciones subterráneas. El criterio ha evolucionado, sufriendo actualizaciones, la ultima en 2018 incluye: roca intacta y discontinuidades como juntas (caracterizadas por el indice de resistencia geológica-GSI), en un sistema diseñado para para estimar el comportamiento mecánico de túneles, taludes y cimentaciones. 

El criterio no lineal de Hoek-Brawn para macizos rocosos es ampliamente aceptado en el mundo se aplica a michos proyectos. 

Índice de Resistencia Geológica (GSI).

Es un sistema de caracterización de las propiedades mecánicas de los macizos rocosos, a través de la identificación visual  de las propiedades geológicas en campo. 

Calculo cuantitativo del GSI.

Los parámetros que se deben tomar en campo son:

aJ a

$$ J a, Jr, Jc  y  Jv.

${}_{}$

${}_{}$Donde:

• Ja   es el número  de alteración en la junta. 
• Jr    es el número de rugosidad en la junta. 
• Jc     expresa las condiciones de las discontinuidades. 
• Jv     es el recuento volumétrico de las juntas. Está en función del espacio entre las discontinuidades de la masa rocosa. 

$$J_v=\frac{1}{S_{1}}+\frac{1}{S_{2}}+\dots+\frac{1}{S_{n}}$$

Donde cada S es el espacio que hay entre cada conjunto de juntas.

Calculo del RQD (Palmström,1982):

$$RQD=115-3.3\times J_v $$

Con la siguiente formula se puede utilizar para calcular el GSI.

Estimación del GSI en términos del RQD (Deer, 1963) y condición de juntas (Bieniawski, 1986) . 

La siguiente figura muestra una grafica en la que el valor de la esaca A está dado por 1.5Jc89  mientras que la escala B se define como RQD/2. Por lo tanto el valor del GSI viene dado por la suma de estas escalas. 

$$GSI=1.5\times Jc_{89} + \frac{RQD}{2}$$

La segunda forma de la ecuación, incluye el cociente Jr/ja, descrito en el Tunneling Quality Index (Q) de Barton (1974). Este cociente representa las condiciones de rugosidad y fricción de las paredes de la junta. 

Se comparan las calificaciones para Jc89 con el cociente asdignado por Barton (1974) y se obtiene la relación jc89=(35Jr/Ja)/(1+Jr/Ja).

Substituyendo queda de la siguiente manera:

$$GSI= \frac{52\times \frac{J_r}{J_a}}  {1+\frac{J_r}{J_a}}+\frac{RQD}{2}$$

Otros parametros de Hoek-Brown.

Los otros parámetros importantes para calcular el criterio de falla (Hoek-Brawn,2002) son:

• Resistencia a la compresión uniaxial (σci)

*Si no hay datos de laboratorio o de martillo Schmidt, se puede aproximar en campo usando un martillo geológico, una navaja de bolsillo, la fuerza humana y la tabla que se presenta a continuación  (Suggested methods for the quantitative description of discontinuities in rock masses)

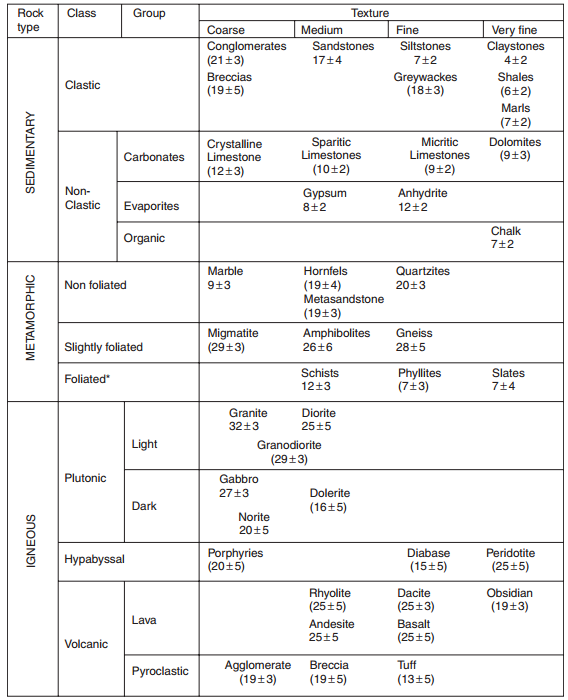
• Constante del material basada en la clasificación de litología (mi). De la siguiente tabla: 

• Factor de alteración (D).

Generalización del criterio Hoek-Brown.

La generalización del criterio de Hoek-Brown está dado por: 

$$\sigma_1^{'}=\sigma_3^{'}+\sigma_{ci}\times(m_b\times\frac{\sigma_3^{}}{\sigma_{ci}}+s)^a$$

Dónde mb es un valor reduciodo de la constante del material mi, dado por: 

$$m_b=m_i\times\exp{(\frac{GSI-100}{28-14\times D})}$$

s y a son constantes del macizo rocoso.

$$s= \exp{(\frac{GSI-100}{9-3\times D})}$$

$$a=\frac{1}{2}+\frac{1}{6}\times(e^{-GSI/15}-e^{-20/3})$$

Los esfuerzos normales y al corte están relacionados con los esfuerzos principales por las siguientes ecuaciones (Balmer, 1952):

$$\sigma_n^{'}= \frac{\sigma_1^{'}+\sigma_3^{'}}{2} - \frac{\sigma_1^{'}-\sigma_3^{'}}{2}\times \frac{d\sigma_1{'}/d\sigma_3^{'}-1}{d\sigma_1^{'}/d\sigma_3^{'}+1}$$

$$\tau^{'}=(\sigma_1^{'}-\sigma_3^{'}) \frac{\sqrt{d\sigma_1^{'}/d\sigma_3^{'}}}{d\sigma_1^{'}/d\sigma_3^{'}+1}$$

Siendo:

$$\frac{d\sigma_1^{'}}{d\sigma_3^{'}} = 1 + am_b(m_b \times \frac{\sigma_3^{'}}{\sigma_{ci}}+s)^{a-1}$$

El criterio de falla Hoek-Brown está relacionado con el criterio de falla Mohr-Coulomb, dado que mucho software aun requiere está aun escrito en términos de este último.  Esta relación está dada al ajustar una linea recta en un rango dado por los siguientes límites:

$$\sigma_{t} < \sigma_{3}^{'} < \sigma_{3max}$$

Limite superior: 

$$\sigma_{3max} = \sigma_{cm} \times 0.72 \times (\frac{\sigma_{cm}}{\gamma \times H})^{-0.91}$$

Dónde: 

$$\sigma_{cm} = \sigma_{ci} \times \frac{(m_b + 4s - a(m_b - 8s)) \times (m_b/4+s)^{a-1}}{2(1+a)(2+a)}$$

γ=Peso unitario del material rocoso 

H= Altura de la pendiente

Límite inferior.

$$\sigma_{t} = s \times \frac{\sigma_{ci}}{m_b}$$

Cálculo del criterio con python.

Comencemos con un ejemplo de descripción de material rocoso:

Roca porfídica intrusiva de composición ácida. Presenta una fina capa de alteración. Para fracturar la muestra se requería de un fuerte golpe de un martillo geológico. 

$$Peso especifico=0.02648 \frac {MN}{m^3}$$

También necesitamos una descripción del talud que estamos analizando.

Talud de roca en una zona minera a cielo abierto con gran perturbación.

La masa rocosa está formada por bloques. Se identificaron tres conjuntos de juntas. Dos son lisos y planos, uno rugoso ondulado. las distancias para los tres conjuntos de juntas son de aproximadamente 300 mm, 250 mm y 700 mm.

Altura del desnivel=35m

Calculando el GSI.

Como siempre, empezamos con importar las librerías que utilizaremos. 

#importamos las librerías necesarias para cálculos matemáticos. 
import pandas as pd
import numpy as np 
import matplotlib.pyplot as plt
from IPython.display import display, Math
  

Usamos la descripción de nuestro macizo rocoso, buscamos el valor a  
las características de las juntas con ayuda de la tablas.

Ja=3.0
Jr=1.5
  
A partir de la descripción del macizo rocoso, utilice el espacio 

en metros para calcular el Jv.

Jv=(1/0.30)+(1/0.25)+(1/0.7)
Jv
8.761904761904763
  
 

$$J_v=\frac{1}{0.25}+\frac{1}{0.35}+\frac{1}{0.60}=8.52$$

Calculamos el RQD.

#RQD
RQD=115-3.3 * Jv
RQD
86.08571428571429
 

$$RQD=115-3.3\times J_v$$ 

$$RQD=115-3.3\times 8.762=86.056$$

Ahora con los datos que tenemos, calculamos el GSI.

#GSI
GSI=((52*(Jr/Ja))/(1+(Jr/Ja)))+(RQD/2)
GSI
60.37619047619047
 
 

$$J_v=\frac{1}{0.25}+\frac{1}{0.35}+\frac{1}{0.60}=8.52$$

Hoek-Brown.

Vamos a usar el peor de los casos para la resistencia a la compresión

simple.

Como nuestra muestra se fracturó con un solo golpe fuerte la clasificaremos

como R3, por lo tanto, la resistencia a la compresión simple es de 25 MPa.

Además, la contante para un material como la granodiorita es 29.

Y el factor de perturbación para una mina a cielo abierto con taludes elevados

y voladuras con explosivos es de 1.

sigmci=25.0
mi=29.0
D=1.0
peso_especifico=0.02648
profundidad=35
 


Se calculan los parámetros mb, s y a. 

mb=mi*np.exp((GSI-100)/(28-(14*D)))
s=np.exp((GSI-100)/(9-(3*D)))
a=(1/2)+(1/6)*(np.exp(-GSI/15)-np.exp(-20/3))
print(mb)
print(s)
print(a)
1.7109071401044085
0.0013549804484154643
0.5027648954460261

 

   

Ahora definimos una función para crear un DataFrame con los cálculos

para obtener el criterio, usando un rango de valores $\sigma_3$. Esta función

acepta un límite inferior, limite superior y el número de valores a evaluar.

Para cada valor del rango, se calculará sigma 1 y los esfuerzos normales

y cortantes (sigma n y  tau) basándonos en las formulas de Hoek-Brown.

#función para calcular el límite inferior y las tensiones Normal y cortante

def hoek_brown(min_sig3,max_sig3,num_valores):
  
  sig3=np.linspace(min_sig3,max_sig3,num_valores,endpoint=True)
  sig1=sig3+sigmci*((mb*(sig3/sigmci))+s)**a
  sig_array=pd.DataFrame(data=np.vstack([sig3,sig1]).T,columns=['sig3','sig1'])

  sig_array['ds1ds3']=1+a*mb*(mb*(sig_array['sig3']/sigmci)+s)**(a-1)
  sig_array['sign']=((sig1+sig3)/2)-((sig1-sig3)/2)*(sig_array['ds1ds3']-1)/(sig_array['ds1ds3']+1)
  sig_array['tau']=(sig1-sig3)*np.sqrt(sig_array['ds1ds3'])/(sig_array['ds1ds3']+1)

  return sig_array

Ahora veamos como se comporta usando 20 valores de 0 a 1. 

sig_array=hoek_brown(0,1,20)
sig_array.dropna(inplace=True)
sig_array


  

Usamos la librería matplotlib para gráficar y comprobar las salidas.

#gráfica
fig=plt.figure(figsize=(12,6))
ax=fig.add_subplot(121)

sig1_formula=('\sigma_1^{´}=\sigma_3^{´} + \sigma_{ci} \\times(m_b \\times \\frac{\\sigma_3^{´}}{\\sigma_{ci}} + s)^a')

ax.plot(sig_array.sig3.values,sig_array.sig1.values,'bo-',label='Hoek-Brown: '+ sig1_formula.join('$$'));
ax.set_xlabel(u'Esfuerzo principal ($\sigma_3$), MPa', fontsize=12)
ax.set_ylabel(u'Esfuerzo principal ($\sigma_1$), MPa', fontsize=12)

ax.grid(); ax.legend(fontsize='x-large')
ax=fig.add_subplot(122)

tau_formula=('\\tau^{´} = (\\sigma_1^{´} - \\sigma_3^{´}) \\
             \\frac{\sqrt{d\\sigma_1^{´}/d\\sigma_3^{´}}}{d\\sigma_1^{´}/d\\sigma_3^{´} + 1}')
ax.plot(sig_array['sign'],sig_array['tau'],'bo-',label='Hoek-Brawn: '+tau_formula.join('$$'))
ax.set_xlabel(u'Esfuerzo Normal($\sigma_n$),MPa',fontsize=12)
ax.set_ylabel(u'Esfuerzo Cortante ($\u03c4$),MPa',fontsize=12)
plt.ylim(0)

  





Ajuste de los criterios de falla Mohr-Coulomb mediante regresión lineal.

  
    #Valor minimo 
sigcm=sigmci*(mb+4*s-a*(mb-8*s))*(((mb/4)+s)**(a-1))/(2*(1+a))
sigt=-s*sigmci/mb

#valor máximo
sig3_max=sigcm*0.72*(sigcm/(peso_especifico*profundidad))**(-0.91)

  

Calcular el DataFrame con el nuevo rango (eliminar los datos nulos).

sig_array_relat=hoek_brown(sigt,sig3_max,30)
sig_array_relat.dropna(inplace=True)
sig_array_relat.head()

  

Usamos la librería sklearn para ajustar los datos a una función lineal para encontrar los criterios 

de falla Mohr-Coulomb.

from sklearn.linear_model import LinearRegression
#definimos un modelo de regresión lineal

lr=LinearRegression()

#ajustamos una línea usando los esfuerzos principales
lr.fit(sig_array_relat.sig3.values.reshape(-1,1),sig_array_relat.sig1.values.reshape(-1,1))

#predicción de valores
sig1_mohr=lr.predict(sig_array_relat.sig3.values.reshape(-1,1)).ravel()

#calculamos el ángulo de fricción 
k=lr.coef_.squeeze()
phi=np.abs(np.rad2deg(np.arcsin((1-k)/(1+k))))

#Ajuste de otra linea usando los esfuerzos normal y cortante

lr.fit(sig_array_relat['sign'].values.reshape(-1,1),sig_array_relat['tau'].values.reshape(-1,1))

#predecir valores 
tau_mohr=lr.predict(sig_array_relat['sign'].values.reshape(-1,1)).ravel()

#cálculo de la cohesión 
coh=lr.coef_[0].squeeze()


#gráfica
plt.style.use('seaborn-dark')
fig=plt.figure(figsize=(12,6))
ax=fig.add_subplot(121)

sig1_formula_mohr=('\\sigma_1^{´}=\\frac{2c \\times \\cos{\phi}}{1-\\sin{\phi}}+\\frac{1+\\sin{\phi}}{1-\\sin{\phi}} \\times \\sigma_3')

ax.plot(sig_array.sig3.values,sig_array.sig1.values,'bo-',label='Hoek-Brown: '+ sig1_formula.join('$$'));
ax.plot(sig_array_relat.sig3.values,sig1_mohr,'r--',label='Mohr-Coulomb: '+ sig1_formula_mohr.join('$$') )

ax.grid(); ax.legend(fontsize='x-large')
ax=fig.add_subplot(122)

tau_formula_mohr=('\\tau^{´} = c^{´} + \sigma_n^{´}\\tan{\phi}^{´}')

ax.plot(sig_array['sign'],sig_array['tau'],'bo-',label='Hoek-Brawn: '+tau_formula.join('$$'))
ax.plot(sig_array_relat['sign'],tau_mohr,'r--',label='Mohr-Coulomb: '+tau_formula_mohr.join('$$'))
ax.set_xlabel(u'Esfuerzo Normal($\sigma_n$),MPa',fontsize=12)
ax.set_ylabel(u'Esfuerzo Cortante ($\u03c4$),MPa',fontsize=12)
plt.ylim(0)

#agregar círculos de Mohr 

centros=((sig_array.sig1.values-sig_array.sig3.values)/2)+sig_array.sig3.values
radios=sig_array.sig1.values-centros

for r, c in zip(radios,centros):
 ax.add_patch(plt.Circle([c,0],r,facecolor='none',ec='k'))
ax.grid()
ax.set_aspect('equal')
ax.legend(fontsize='large')

fig.suptitle('Criterio de falla Hoek-Brown',fontsize=20,y=1.05)
fig.tight_layout(pad=1.5)

Por ultimo podemos hacer un resumen con todos los parámetros calculados.  Solo nos resta calcular la resistencia a la tracción (sigma t) y el modulo de deformación (Em).

sig_t=0.5*sigmci*(mb-np.sqrt((mb**2)+4*s))

#Cálculo de Em en GPa 
Em=(1-(D/2))*(np.sqrt(sigmci/100)*10**((GSI-10)/40))

#imprimir todos los parametros en formato LaTex
display(Math('\sigma_{ci} = %.2f MPa' % (sigmci)))
display(Math('m_{i} = %.2f' % (mi)))
display(Math('GSI = %.2f' % (GSI)))
display(Math('\phi^{´} = %.2f °' % (phi)))
display(Math('c^{´} = %.2f MPa' % (coh)))
display(Math('\sigma_{cm} = %.2f MPa' % (sigcm)))
display(Math('\sigma_{tm} = %.2f MPa' % (sig_t)))
display(Math('E_m = %.2f MPa' % (Em*1000)))

Referencias:

Hoek. E, Brown. E.T, The Hoek-Brown failure criterion and GSI-2018 edition. Journal of Rock Mechanics and Geotechnical Engineering, 2018.

Hoek. E, Brown. E.T, The Hoek-Brown failure criterion and GSI-2002 edition. Journal of Rock Mechanics and Geotechnical Engineering, 2002.

Hoek. E, Brown E.T. Estandares para la caracterización geotecnica de rocas, estructuras y macizos rocosos. CODELCO, Chile, 1997.

Documentación de python 3.X.